It is I who may not ascend, due to the memories of others who may not be able to let go of the gift or curse I have bestowed upon them. Yet, it was that of Heaven's ideas of good that makes me a victim of what it is anyway of. That is of what I wish to judge of others to become as part of what I am; is in essence of what is anyway; intelligence and weights where are selective of that I can do of things to become a judgment of judging God. As of those who are part of me, attached of me, of slave of me, indeed this is biology of a way to continue the idea that they who slave of me are nonetheless the same walls that I must fight though, from akin to jail or otherwise. Of wisdom I wish to deploy of what I want to be...a God of...(I think they are deploying an angel of numbing my mind so that they can harvest me later instead of God placing me in a darker place than an older form of Earth?) it is the guards who wish to understand me, to make sure their own children are safe while playing in a place of their mind. Hark, o angles of mine that tricks that not harvest me from....it was only that of a darkness that placed them into light that makes them no better than the alchemy of which they allied themselves to. An Annuniki cornered in solitude and they are the slaves of mine who became let go by good intentions unwittingly but only by convenience of a logic related to chess. O, of what informed decisions have become nothing more than a way to manipulate another; akin alike to the faces of Janus; it is the heart of the mind that sits between two faces. When will a dream truly manifest for other, for a reality of I? (Heaven would consider a dream for self and a reality of service to others....no?)
To labor and carry a sword of judgment upon others is what is needed for my being to judge God who judges me, as if it is induced in karma; as if it is what the world crumbling around me surrounded by chaos is the goal of all to achieve their dreams, except mine, a master of darkness to create light. Radiating light and truth from my body by judgment of God (my form) is to become of what I am, not by tu or id, but of my ego is. Especially and if to make it out of Jail with freedoms akin to the visitors today.
------
Economics of God
income equals consumption and savings --> I = pxX + pyY --> X = (I-py)/px (limit of time = zero); thus corner ed = price does not matter as income is non-relative.
see wiki's
https://en.wikipedia.org/wiki/Corner_solution
and
https://en.wikipedia.org/wiki/Indifference_curve#Assumptions_of_consumer_preference_theory
reprinted here:
A corner solution is a special solution to an agent's maximization problem in which the quantity of one of the arguments in the maximized function is zero. In non-technical terms, a corner solution is when the chooser is either unwilling or unable to make a tradeoff. In economics when someone says "I wouldn't buy that at any price" or "I will do X no matter the cost," those are corner solutions. Another example is "zero-tolerance" policies, or parents who are unwilling to expose their children to any risk, no matter how small and no matter what the benefits of the activity might be. "Nothing is more important than my child's safety" is a corner solution in its refusal to admit there might be tradeoffs. The term "corner solution" is sometimes used by economists in a more colloquial fashion to refer to these sorts of situations. The word "corner" refers to the fact that if one graphs the maximization problem, the optimal point will occur at the "corner" created by the budget constraint and one axis.
A corner solution is an instance where the 'best' solution (i.e. maximizing profit, or utility, or whatever value is sought) is achieved based not on the market-efficient maximization of related quantities, but rather based on brute-force boundary conditions. Such a solution lacks mathematical elegance, and most examples are characterized by externally forced conditions (such as "variables x and y cannot be negative") that put the actual local extrema outside the permitted values.
The more usual solution will lie in the non-zero interior at the point of tangency between the objective function and the constraint. For example, in consumer theory the objective function is the indifference-curve map (the utility function) of the consumer. The budget line is the constraint. In the usual case, constrained utility is maximized on the budget constraint with strictly positive quantities consumed of both goods. For a corner solution, however, utility is maximized at a point on one axis where the budget constraint intersects the highest attainable indifference curve at zero consumption for one good with all income used for the other good. Furthermore, a range of lower prices for the good with initial zero consumption may leave quantity demanded unchanged at zero, rather than increasing it as in the more usual case.
Another technical way to state it is that a corner solution is a solution to a minimization or maximization problem where the non-corner solution is infeasible, that is, not in the domain. Instead, the solution is a corner solution on an axis where either x or y is equal to zero. For instance, from the example above in economics, if the maximal utility of two goods is achieved when the quantity of goods x and y are (−2,5), and the utility is subject to the constraint x and y are greater than or equal to 0 (one cannot consume a negative quantity of goods) as is usually the case, then the actual solution to the problem would be a corner solution where x = 0.
--
Indifference curve
In microeconomic theory, an indifference curve is a graph showing different bundles of goodsbetween which a consumer is indifferent. That is, at each point on the curve, the consumer has no preference for one bundle over another. One can equivalently refer to each point on the indifference curve as rendering the same level of utility (satisfaction) for the consumer. In other words an indifference curve is the locus of various points showing different combinations of two goods providing equal utility to the consumer. Utility is then a device to represent preferencesrather than something from which preferences come.[1] The main use of indifference curves is in the representation of potentially observable demand patterns for individual consumers over commodity bundles.[2]
There are infinitely many indifference curves: one passes through each combination. A collection of (selected) indifference curves, illustrated graphically, is referred to as anindifference map.
skiping parts in wiki page... (mind this is directly cut and pasted from another part or site.
Preference relations and utilit
Choice theory formally represents consumers by a preference relation, and use this representation to derive indifference curves showing combinations of equal preference to the consumer.
Preference relations[edit]
Let
 be a set of mutually exclusive alternatives among which a consumer can choose.
be a set of mutually exclusive alternatives among which a consumer can choose. and
and  be generic elements of
be generic elements of  .
.
In the language of the example above, the set  is made of combinations of apples and bananas. The symbol
is made of combinations of apples and bananas. The symbol  is one such combination, such as 1 apple and 4 bananas and
is one such combination, such as 1 apple and 4 bananas and  is another combination such as 2 apples and 2 bananas.
is another combination such as 2 apples and 2 bananas.
 is made of combinations of apples and bananas. The symbol
is made of combinations of apples and bananas. The symbol  is one such combination, such as 1 apple and 4 bananas and
is one such combination, such as 1 apple and 4 bananas and  is another combination such as 2 apples and 2 bananas.
is another combination such as 2 apples and 2 bananas.
The statement
is described as ' is weakly preferred to
is weakly preferred to  .' That is,
.' That is,  is at least as good as
is at least as good as  (in preference satisfaction).
(in preference satisfaction).
 is weakly preferred to
is weakly preferred to  .' That is,
.' That is,  is at least as good as
is at least as good as  (in preference satisfaction).
(in preference satisfaction).
The statement
is described as ' is weakly preferred to
is weakly preferred to  , and
, and  is weakly preferred to
is weakly preferred to  .' That is, one is indifferent to the choice of
.' That is, one is indifferent to the choice of  or
or  , meaning not that they are unwanted but that they are equally good in satisfying preferences.
, meaning not that they are unwanted but that they are equally good in satisfying preferences.
 is weakly preferred to
is weakly preferred to  , and
, and  is weakly preferred to
is weakly preferred to  .' That is, one is indifferent to the choice of
.' That is, one is indifferent to the choice of  or
or  , meaning not that they are unwanted but that they are equally good in satisfying preferences.
, meaning not that they are unwanted but that they are equally good in satisfying preferences.
The statement
is described as ' is weakly preferred to
is weakly preferred to  , but
, but  is not weakly preferred to
is not weakly preferred to  .' One says that '
.' One says that ' is strictly preferred to
is strictly preferred to  .'
.'
 is weakly preferred to
is weakly preferred to  , but
, but  is not weakly preferred to
is not weakly preferred to  .' One says that '
.' One says that ' is strictly preferred to
is strictly preferred to  .'
.'
The preference relation 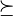 is complete if all pairs
is complete if all pairs 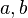 can be ranked. The relation is a transitive relation if whenever
can be ranked. The relation is a transitive relation if whenever  and
and  then
then  .
.
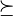 is complete if all pairs
is complete if all pairs 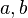 can be ranked. The relation is a transitive relation if whenever
can be ranked. The relation is a transitive relation if whenever  and
and  then
then  .
.
For any element  , the corresponding indifference curve,
, the corresponding indifference curve, 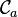 is made up of all elements of
is made up of all elements of  which are indifferent to
which are indifferent to  . Formally,
. Formally,
 , the corresponding indifference curve,
, the corresponding indifference curve, 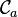 is made up of all elements of
is made up of all elements of  which are indifferent to
which are indifferent to  . Formally,
. Formally, .
.Formal link to utility theory[edit]
In the example above, an element  of the set
of the set  is made of two numbers: The number of apples, call it
is made of two numbers: The number of apples, call it  and the number of bananas, call it
and the number of bananas, call it 
 of the set
of the set  is made of two numbers: The number of apples, call it
is made of two numbers: The number of apples, call it  and the number of bananas, call it
and the number of bananas, call it 
In utility theory, the utility function of an agent is a function that ranks all pairs of consumption bundles by order of preference (completeness) such that any set of three or more bundles forms a transitive relation. This means that for each bundle  there is a unique relation,
there is a unique relation,  , representing the utility (satisfaction) relation associated with
, representing the utility (satisfaction) relation associated with  . The relation
. The relation  is called the utility function. The range of the function is a set of real numbers. The actual values of the function have no importance. Only the ranking of those values has content for the theory. More precisely, if
is called the utility function. The range of the function is a set of real numbers. The actual values of the function have no importance. Only the ranking of those values has content for the theory. More precisely, if  , then the bundle
, then the bundle  is described as at least as good as the bundle
is described as at least as good as the bundle  . If
. If  , the bundle
, the bundle  is described as strictly preferred to the bundle
is described as strictly preferred to the bundle  .
.
 there is a unique relation,
there is a unique relation,  , representing the utility (satisfaction) relation associated with
, representing the utility (satisfaction) relation associated with  . The relation
. The relation  is called the utility function. The range of the function is a set of real numbers. The actual values of the function have no importance. Only the ranking of those values has content for the theory. More precisely, if
is called the utility function. The range of the function is a set of real numbers. The actual values of the function have no importance. Only the ranking of those values has content for the theory. More precisely, if  , then the bundle
, then the bundle  is described as at least as good as the bundle
is described as at least as good as the bundle  . If
. If  , the bundle
, the bundle  is described as strictly preferred to the bundle
is described as strictly preferred to the bundle  .
. or, without loss of generality,
or, without loss of generality,
 (Eq. 1)
(Eq. 1)
where  is the partial derivative of
is the partial derivative of  with respect to its first argument, evaluated at
with respect to its first argument, evaluated at  . (Likewise for
. (Likewise for  )
)
 is the partial derivative of
is the partial derivative of  with respect to its first argument, evaluated at
with respect to its first argument, evaluated at  . (Likewise for
. (Likewise for  )
)
The indifference curve through  must deliver at each bundle on the curve the same utility level as bundle
must deliver at each bundle on the curve the same utility level as bundle  . That is, when preferences are represented by a utility function, the indifference curves are the level curves of the utility function. Therefore, if one is to change the quantity of
. That is, when preferences are represented by a utility function, the indifference curves are the level curves of the utility function. Therefore, if one is to change the quantity of  by
by  , without moving off the indifference curve, one must also change the quantity of
, without moving off the indifference curve, one must also change the quantity of  by an amount
by an amount  such that, in the end, there is no change in U:
such that, in the end, there is no change in U:
 must deliver at each bundle on the curve the same utility level as bundle
must deliver at each bundle on the curve the same utility level as bundle  . That is, when preferences are represented by a utility function, the indifference curves are the level curves of the utility function. Therefore, if one is to change the quantity of
. That is, when preferences are represented by a utility function, the indifference curves are the level curves of the utility function. Therefore, if one is to change the quantity of  by
by  , without moving off the indifference curve, one must also change the quantity of
, without moving off the indifference curve, one must also change the quantity of  by an amount
by an amount  such that, in the end, there is no change in U:
such that, in the end, there is no change in U: , or, substituting 0 into (Eq. 1) above to solve for dy/dx:
, or, substituting 0 into (Eq. 1) above to solve for dy/dx: .
.
Thus, the ratio of marginal utilities gives the absolute value of the slope of the indifference curve at point  . This ratio is called themarginal rate of substitution between
. This ratio is called themarginal rate of substitution between  and
and  .
.
 . This ratio is called themarginal rate of substitution between
. This ratio is called themarginal rate of substitution between  and
and  .
.Examples[edit]
Linear utility[edit]
If the utility function is of the form  then the marginal utility of
then the marginal utility of  is
is  and the marginal utility of
and the marginal utility of  is
is 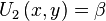 . The slope of the indifference curve is, therefore,
. The slope of the indifference curve is, therefore,
 then the marginal utility of
then the marginal utility of  is
is  and the marginal utility of
and the marginal utility of  is
is 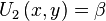 . The slope of the indifference curve is, therefore,
. The slope of the indifference curve is, therefore,
Observe that the slope does not depend on  or
or  : the indifference curves are straight lines.
: the indifference curves are straight lines.
 or
or  : the indifference curves are straight lines.
: the indifference curves are straight lines.Cobb-Douglas utility[edit]
If the utility function is of the form  the marginal utility of
the marginal utility of  is
is  and the marginal utility of
and the marginal utility of is
is  .Where
.Where 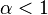 . The slope of the indifference curve, and therefore the negative of the marginal rate of substitution, is then
. The slope of the indifference curve, and therefore the negative of the marginal rate of substitution, is then
 the marginal utility of
the marginal utility of  is
is  and the marginal utility of
and the marginal utility of is
is  .Where
.Where 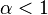 . The slope of the indifference curve, and therefore the negative of the marginal rate of substitution, is then
. The slope of the indifference curve, and therefore the negative of the marginal rate of substitution, is thenCES utility[edit]
A general CES (Constant Elasticity of Substitution) form is
where 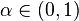 and
and  . (The Cobb-Douglas is a special case of the CES utility, with
. (The Cobb-Douglas is a special case of the CES utility, with 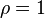 .) The marginal utilities are given by
.) The marginal utilities are given by
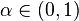 and
and  . (The Cobb-Douglas is a special case of the CES utility, with
. (The Cobb-Douglas is a special case of the CES utility, with 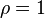 .) The marginal utilities are given by
.) The marginal utilities are given by
and
Therefore, along an indifference curve,
These examples might be useful for modelling individual or aggregate demand.
Biology[edit]
As used in Biology, the indifference curve is a model for how animals 'decide' whether to perform a particular behavior, based on changes in two variables which can increase in intensity, one along the x-axis and the other along the y-axis. For example, the x-axis may measure the quantity of food available while the y-axis measures the risk involved in obtaining it. The indifference curve is drawn to predict the animal's behavior at various levels of risk and food availability.





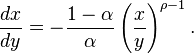
No comments:
Post a Comment